Which Table Represents a Linear Function? (With Easy Examples & Quick Test)

Bitcraft production, Apr 20, 2025, Education
Which Table Represents a Linear Function? (With Easy Examples & Quick Test)

Have you ever looked at a table of numbers and wondered,
“Is this a linear function?” Let’s break it down in a simple way.
With easy rules.
And quick examples.

What is a Linear Function?

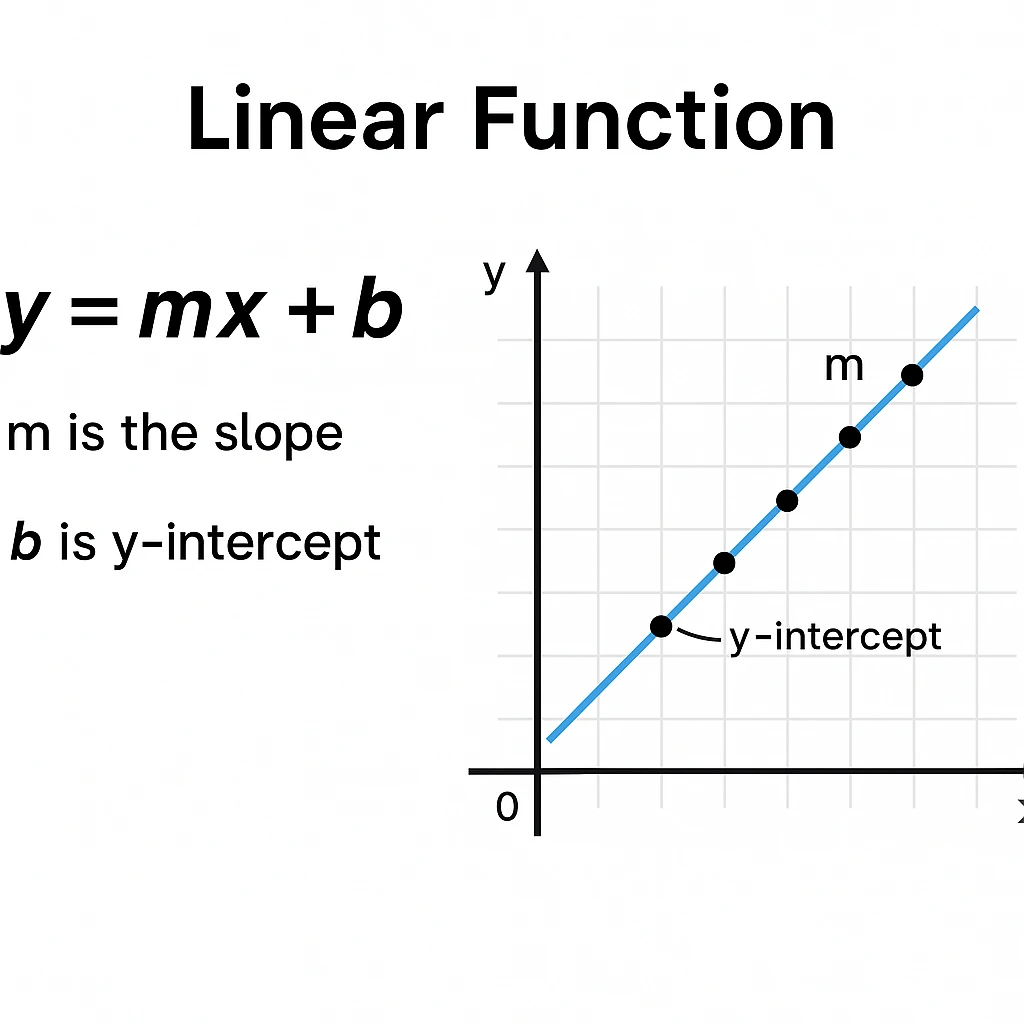
A linear function is a rule that creates a straight line when you graph it.
It follows the form:

y = mx + b
  • m is the slope (the rate of change)
  • b is the y-intercept

How to Tell from a Table

To find out if a table shows a linear function, use this rule:

Check if the change in y is always the same when x changes by the same amount.

This is called a constant rate of change.

Let’s Try an Example

Here’s a table:

x y
1 3
2 5
3 7
4 9

Let’s check:

  • From x=1 to x=2 → y goes from 3 to 5 → change is +2
  • From x=2 to x=3 → y goes from 5 to 7 → change is +2
  • From x=3 to x=4 → y goes from 7 to 9 → change is +2

✅ The change in y is always +2
So, this table represents a linear function.

Another Example: Is This Linear?

Let’s look at this new table:

x y
2 6
4 10
6 14
8 18

Let’s check the changes step by step.

Step 1: Change in x

  • From 2 → 4 → 6 → 8
  • Change in x is +2 every time.

Step 2: Change in y

  • From 6 → 10 → 14 → 18
  • Change in y is +4 every time.

Now check:

Change in y ÷ change in x = 4 ÷ 2 = 2

Since the ratio is the same every time,
✅ this table represents a linear function.

A Non-Example (Not Linear)

x y
1 2
2 4
3 8
4 16

Check the y changes:

  • +2 → +4 → +8 → it’s not the same

This is not a linear function
It’s probably an exponential function.

Quick Trick to Remember

If the difference in y is always the same,
and the difference in x is also the same,
✅ it’s linear!

Also Read: ACT Math Formulas

Quick Test: Which Table is Linear?

Here are two tables.
Which one is linear?

Table A:

x y
1 5
2 8
3 11
4 14

Table B:

x y
1 1
2 4
3 9
4 16

Answer: Table A is linear
Because y increases by +3 each time. Now, find the answer for table B.

Summary

  • A linear function has a constant rate of change
  • Check if y changes evenly when x increases evenly
  • Use this to spot linear tables easily

Want More Help Like This?

Try Study Friend — your AI-powered study buddy.

  • Get quick answers
  • Generate flashcards
  • Build mindmaps
  • Track your learning

👉 Download Study Friend Now

FAQ: Linear Function from a Table

1. How do you know if a table shows a linear function?

Check if the change in y is always the same when x changes by the same amount.

2. What is a constant rate of change?

A constant rate of change means y changes by the same amount every time x increases by a fixed number.

3. Can a table with unequal x values still be linear?

Yes, as long as the rate of change (Δy/Δx) stays the same.

4. What does a nonlinear table look like?

The changes in y are not consistent. For example: +1, +3, +7, +13.

5. What if y is always the same?

That’s still linear! It’s called a horizontal line (slope = 0).